3.4.1 PUNTOS DE INFLEXION

Se define un punto de inflexión como el punto en que la función pasa de ser convexa a cóncava o de cóncava a convexa.

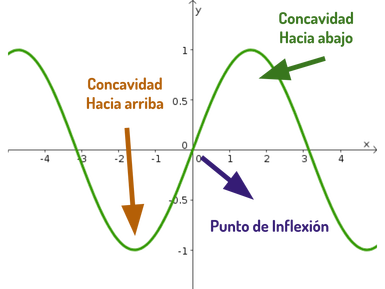
En la siguiente gráfica podemos ver que cuando x = 0, la gráfica pasa de ser cóncava a ser convexa, por lo que podemos decir que el punto de inflexión esta en X = 0.

Una característica de los puntos de inflexión es que son los puntos donde la función derivada tiene máximos y mínimos. Si nos fijamos, cuando nos acercamos a un punto de inflexión la función cada vez crece más (o decrece menos), pero al sobrepasar el punto de inflexión la función empieza a crecer menos (o decrecer menos). Esto significa que justamente donde haya un punto de inflexión la derivada tendrá un máximo o un mínimo. Consecuentemente encontraremos los puntos de inflexión buscando ceros de la segunda derivada.

Vamos a ilustrar el proceso con un ejemplo para así dar una explicación simple y clara:

Consideraremos la función F(x) = x³ - 3x  (es la función representada en la anterior gráfica).

Sabemos ya calcular los máximos y los mínimos de la función f(x)  usando la primera derivada. La expresión de ésta es 3x² - 3  y justamente encontramos máximos y mínimos respectivamente en x = -14  y x = 1 .  Si representamos la gráfica de la derivada queda:

Observamos que justamente donde la derivada tiene un mínimo es donde la función tiene el punto de inflexión.

Para saber qué punto es vamos a derivar la función derivada e igualarla a cero: F´´(x) = 6x=0 = x = 0/6 = 0, y por tanto la función original en x = 0  tiene un punto de inflexión.

EJEMPLO (PUNTOS  DE INFLEXIÓN)